• Homework Hack

    • Algorithms 2D Array Java

    Objectives:

    Understand how to perform Linear Search in a 2D array.

    Learn to implement Binary Search in a sorted 2D array.

    1. Introduction to Searching in 2D Arrays

    Key Concepts:

    Linear Search: Sequentially checks every element.

    Binary Search: Cuts the search space in half each time, but only works on sorted arrays.

    { { 3, 12, 9 },

    { 5, 2, 89 },

    { 90, 45, 22 } }

    • In the code, you use two nested loops to go through each row [i] and then each column [j] of the 2D array.

    • You start with arr[0][0] (which is 3), then move to arr[0][1] (which is 12), and so on.

    • Linear search checks every element, so it can be slow if you have a huge dataset. It takes O(n*m) time, where n is the number of rows, and m is the number of columns.

    • Why Use It? It works with any array, whether it’s sorted or not.

    Linear Search algorithm

    public class GFG {

    static int[] linearSearch(int[][] arr, int target) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                if (arr[i][j] == target) {
                    System.out.println("Element found");
                    return new int[] { i, j };
                }
            }
        }
        return new int[] { -1, -1 };
    }
    
    public static void main(String[] args) {
        System.out.println("First Line");
        int arr[][] = {
            { 3, 12, 9 },
            { 5, 2, 89 },
            { 90, 45, 22 }
        };
        int target = 89;

        int[] result = linearSearch(arr, target);
        
        if (result[0] != -1) {
            System.out.println("Element found at row " + result[0] + ", column " + result[1]);
        } else {
            System.out.println("Element not found");
        }
    }

    
}
GFG.main(null);

    First Line
Element found
Element found at row 1, column 2

    Explanation:

    • The algorithm goes row by row and column by column until it finds the target value.
    • If the value is found, it returns the index of that element.

    Popcorn Hack 1: Custom 2D Search Challenge

    Question:

    You are given a sorted 5x5 2D array, where each row is sorted in ascending order. Write a function to perform binary search to find a target number in this 2D array. Your function should return both the index of the found element (row and column).

    Requirements:

    Implement a binary search function for the 2D array.

    Function should display the row and column

    The output should display whether the element was found.

    {
    {1, 3, 5, 7, 9},
    {10, 12, 14, 16, 18},
    {20, 22, 24, 26, 28},
    {30, 32, 34, 36, 38},
    {40, 42, 44, 46, 48}
}

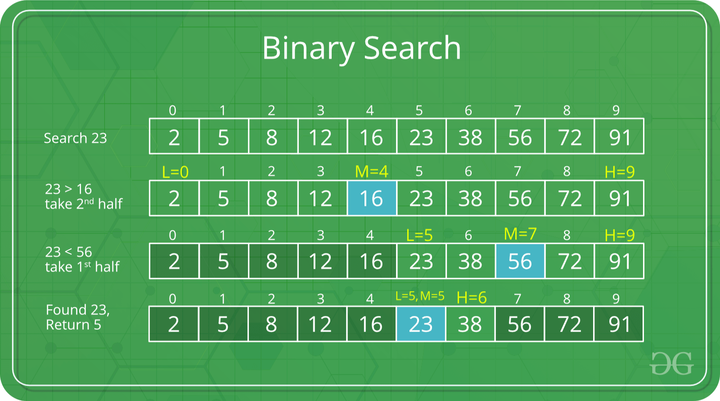
    Binary Search in a 2D Array:

    1. Sorted Array Requirement: Binary search only works on arrays that are sorted in ascending order. If the array is not sorted, the binary search algorithm will not function correctly.

    2. Dividing the Search Space: The algorithm calculates the middle index of the current search range and compares the middle element to the target value:

    { 2, 5, 8, 12, 15, 23, 37, 45, 67 }

    • If the middle element is equal to the target, the search is complete.
    • If the middle element is less than the target, it discards the left half of the array (including the middle element) and continues searching in the right half.
    • If the middle element is greater than the target, it discards the right half of the array and continues searching in the left half.

    Applying Binary Search to a 2D Array:

    When dealing with a 2D array, we can treat the array as a flattened 1D array.

    Think of a 2D array as a long list, you can imagine the 2D array as one single row of values.

    Flattened 2D array

    Finding the position of an element:

    • If you have an element located at (i, j), you can find its position in the long list using this formula:

      • Position = (i * number of columns) + j

    Converting back from a position to (i, j):

    • If you know the position in the long list and want to find out which row and column it corresponds to, use these formulas:

      • Row = Position / number of columns

      • Column = Position % number of columns

    public class Main {
    public static void main(String[] args) {
        // Creating a 2D matrix using sorted array values
        int[][] matrix = {
            {2, 5, 8},
            {12, 15, 23},
            {37, 45, 67}
        };
        int target = 5; // Change this to test with other values like 12, 23, etc.

        // Perform binary search and get the result
        int[] result = binarySearch(matrix, target);

        // Check the result and print appropriate message
        if (result[0] != -1) {
            System.out.println("Target " + target + " found at position: Row " + result[0] + ", Column " + result[1]);
        } else {
            System.out.println("Target " + target + " not found in the matrix.");
        }
    }

    public static int[] binarySearch(int[][] matrix, int target) {
        // Get the number of rows and columns
        int rows = matrix.length;
        int cols = matrix[0].length;

        // Initialize left and right pointers for the search range
        int left = 0;
        int right = rows * cols - 1;

        // Loop until the search range is valid
        while (left <= right) {
            // Calculate the middle index
            int mid = left + (right - left) / 2;
            // Convert the 1D index back to 2D row and column
            int midValue = matrix[mid / cols][mid % cols];

            // Check if the middle value is the target
            if (midValue == target) {
                return new int[] {mid / cols, mid % cols}; // Return the found position
            }

            // Adjust the search range based on the comparison
            if (midValue < target) {
                left = mid + 1; // Search in the right half
            } else {
                right = mid - 1; // Search in the left half
            }
        }

        // Return -1 for both row and column if not found
        return new int[] {-1, -1}; 
    }
}

// To execute the main method, use:
Main.main(null);

    Target 5 found at position: Row 0, Column 1

    Explanation:

    Main Method

    • Initialize a sorted 2D array (matrix) and define a target value to search for
    • Call binarySearch(matrix, target) to find the target’s position.
    • Output the result:
      • If found, print the row and column.
      • If not found, indicate the target is absent.

    Binary Search Method

    • Parameters: Takes a 2D array and a target value.
    • Setup:
      • Get the number of rows and columns.
      • Initialize left (0) and right (last index).
    • Search Loop:
      • While left <= right:
        • Calculate mid index.
        • Convert mid to 2D indices.
        • Check midValue against target:
          • If equal, return indices
          • If less, adjust left
          • If greater, adjust right

    Return {-1, -1} if the target isn’t found.

    2D Array Performing Binary Search

    Popcorn Hack - 2

    Create a program that performs binary search on a sorted 2D array to find a specified target number. Your function should return the position of the target if found, or indicate that the target is not present in the array.

    Common College Board Algorithm Question Types

    There are 3 types of standard algorithms that can be applied upon 2D arrays that are commonly tested by Collegeboard:

    1. Mathematical Analysis: Algorithms that involve performing mathematical operations or calculations on 2D arrays, such as finding sums, averages, or other statistical measures. Examples include calculating the sum of all elements in a matrix or finding the determinant of a matrix.

    2. Analyzing Element Properties: Algorithms that focus on examining and manipulating the properties of individual elements within a 2D array. This might involve checking for specific conditions, such as how many elements are prime, identifying the number of even/odd numbers, or surveying for any other properties.

    3. Reordering Elements: Algorithms that involve changing the order of elements within a 2D array based on certain criteria. This could include sorting rows or columns, rotating the matrix, or rearranging elements to achieve a desired configuration. Examples include sorting the rows of a matrix in ascending order or rotating the matrix 90 degrees clockwise.

    Mathematical Analysis

    /// Define the class named MatrixSum
public class MatrixSum {
    // Entry point of the program
    public static void main(String[] args) {
        // Initialize a 2D array (matrix) with predefined values
        // The matrix here is a 3x3 array with integers from 1 to 9
        int[][] matrix = {
            {1, 2, 3},  // First row of the matrix
            {4, 5, 6},  // Second row of the matrix
            {7, 8, 9}   // Third row of the matrix
        };
        
        // Call the calculateSum method with the matrix as an argument
        // This method will return the sum of all elements in the matrix
        int sum = calculateSum(matrix);
        
        // Print the sum of all elements in the matrix to the console
        // The output will be: "Sum of all elements: 45"
        System.out.println("Sum of all elements: " + sum);

        // Call the test method to execute the tests
        testMatrixSum();
    }

    // Method to calculate the sum of all elements in a 2D matrix
    // This method takes a 2D integer array (matrix) as input and returns an integer (the sum)
    public static int calculateSum(int[][] matrix) {
        // Initialize a variable to hold the sum of the matrix elements
        int sum = 0;
        
        // Iterate over each row in the matrix
        // 'row' represents each 1D array (row) in the 2D array (matrix)
        for (int[] row : matrix) {
            // Iterate over each element in the current row
            // 'element' represents each integer value in the row
            for (int element : row) {
                // Add the current element to the sum
                sum += element;
            }
        }
        
        // Return the final sum after all elements have been added
        return sum;
    }

    // Test method to execute the calculations and print results
    public static void testMatrixSum() {
        // Test 1: Matrix with all positive integers
        int[][] matrix1 = {
            {1, 2, 3},
            {4, 5, 6},
            {7, 8, 9}
        };
        System.out.println("Sum of all elements in matrix 1: " + calculateSum(matrix1));
    }
}
MatrixSum.testMatrixSum();


    Sum of all elements in matrix 1: 45

    Analysis of Properties of a 2D array

    public class PrimeNumberCounter {

    /**
     * Checks if a number is prime.
     * 
     * @param num The number to check.
     * @return true if the number is prime, false otherwise.
     */
    public static boolean isPrime(int num) {
        // Numbers less than or equal to 1 are not prime numbers
        if (num <= 1) return false;
        
        // 2 and 3 are prime numbers
        if (num <= 3) return true;
        
        // Eliminate even numbers greater than 2 and multiples of 3
        if (num % 2 == 0 || num % 3 == 0) return false;
        
        // Check for factors from 5 up to the square root of num
        // Increment by 6 to check numbers of the form 6k ± 1
        for (int i = 5; i * i <= num; i += 6) {
            // Check divisibility by i and i + 2
            if (num % i == 0 || num % (i + 2) == 0) return false;
        }
        
        // If no factors were found, num is prime
        return true;
    }

    /**
     * Counts the number of prime numbers in a 2D array.
     * 
     * @param array The 2D array of integers to check.
     * @return The count of prime numbers in the array.
     */
    public static int countPrimes(int[][] array) {
        int primeCount = 0; // Initialize count of prime numbers

        // Iterate over each row in the 2D array
        for (int[] row : array) {
            // Iterate over each element in the row
            for (int num : row) {
                // Check if the current number is prime
                if (isPrime(num)) {
                    primeCount++; // Increment count if prime
                }
            }
        }

        // Return the total count of prime numbers
        return primeCount;
    }
}

// Test the PrimeNumberCounter class
public class TestPrimeNumberCounter {
    public static void main(String[] args) {
        // Define a 2D array of integers for testing
        int[][] testArray = {
            {2, 4, 7, 8},
            {11, 13, 17, 19},
            {23, 24, 25, 29},
            {31, 32, 37, 41}
        };

        // Count the number of prime numbers in the test array
        int primeCount = PrimeNumberCounter.countPrimes(testArray);
        // Print the result
        System.out.println("Number of prime numbers: " + primeCount);
    }
}
TestPrimeNumberCounter.main(null);


    Number of prime numbers: 11
    • Asides from the first 2 prime numbers, every other prime number from 1-100 is equivalent to 6k +/- 1 as we can verify in the following image.

    prime_numbers

    Reordering Elements

    public class MatrixRotation {
    public static void main(String[] args) {
        // Initialize a 3x3 matrix
        int[][] matrix = {
            {1, 2, 3},
            {4, 5, 6},
            {7, 8, 9}
        };
        
        // Rotate the matrix 90 degrees clockwise
        int[][] rotated = rotateMatrix90Degrees(matrix);
        
        // Print the rotated matrix
        printMatrix(rotated);
    }

    /**
     * Rotates the given square matrix 90 degrees clockwise.
     * 
     * @param matrix The matrix to be rotated
     * @return The rotated matrix
     */
    public static int[][] rotateMatrix90Degrees(int[][] matrix) {
        int n = matrix.length;  // Get the size of the matrix
        int[][] rotated = new int[n][n];  // Initialize a new matrix for the rotated result
        
        // Perform the rotation
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                // Map the element from the original matrix to the rotated matrix
                rotated[j][n - 1 - i] = matrix[i][j];
            }
        }
        return rotated;  // Return the rotated matrix
    }
    
    /**
     * Prints the given matrix to the console.
     * 
     * @param matrix The matrix to be printed
     */
    public static void printMatrix(int[][] matrix) {
        // Loop through each row of the matrix
        for (int[] row : matrix) {
            // Loop through each element in the row
            for (int element : row) {
                // Print the element followed by a space
                System.out.print(element + " ");
            }
            // Print a newline after each row
            System.out.println();
        }
    }
}
MatrixRotation.main(null);


    7 4 1 
8 5 2 
9 6 3
    • 90 degree rotation can be seen in how the position of 3 in the original matrix (can be written as (0,2)) becomes (2,-1)
    • note: negative indexing is an important concept to know; -1 means the last element (in this case a value of -1 for the column value means the last column)

    rotate

    Popcorn Hack

    Write a program in Java that allows you to find the number of elements in an array that are less than a certain input k.

    Alternate Resources

    Past CSA FRQs on Algorithms Applied to 2D Arrays

    1. 2014 FRQ - Problem 3: This problem involves working with a 2D array containing names and the number of absences of students. The 2D array has to be traversed and searched for all elements that satisfy a certain property.

    2. 2015 FRQ - Problem 1: This problem requires basic summation of entries in the 2D array and proceeds to require a more mathematically advanced algorithm in part (c).

    3. 2017 FRQ - Problem 4: This FRQ begins with a traversal of a 2D array to find the position of a certain integer and then proceeds to a problem of finding the number of possible subarrays within that grid.

    Homework Hack

    CB 2021 FRQ Question 4a

    Link