Calculator Enactment
Continue with Classes, Queues, performing Sorts and BigO analysis on your algorithm(s).
Lesson: Stack vs Queue Calculator
Introduction
Stacks and Queues are two fundamental data structures that have different methods of adding and removing elements. In this lesson, we will compare Stacks and Queues and explore how they can be used to implement a calculator. —
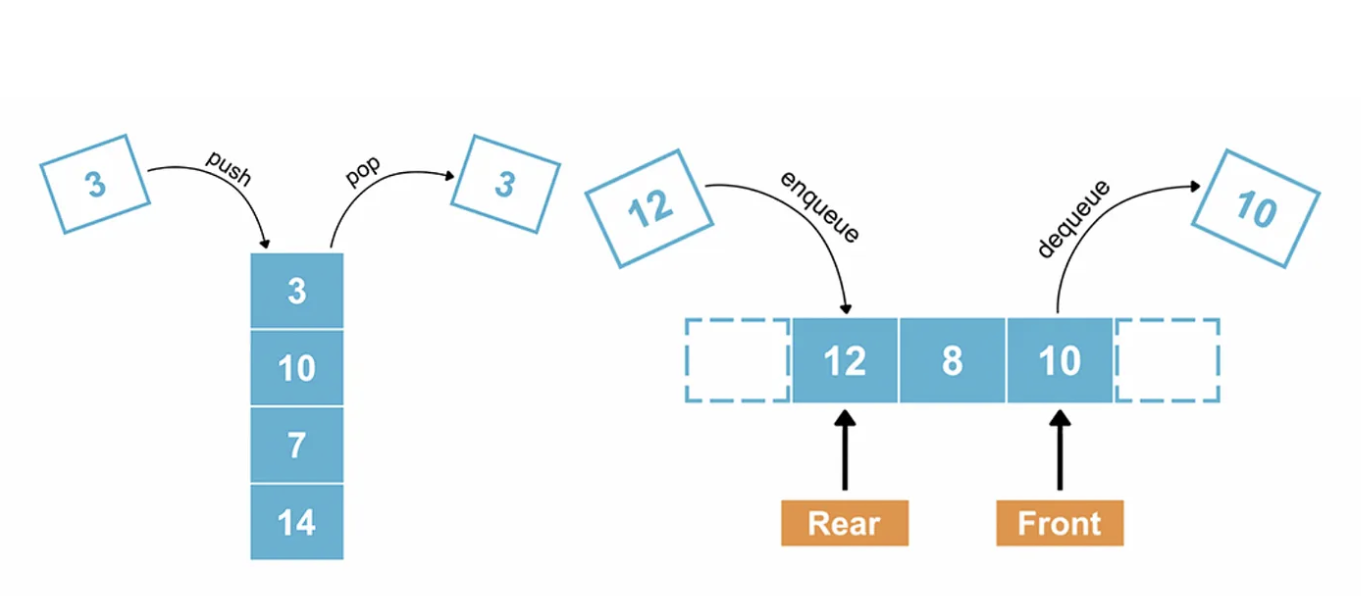
What is a Stack?
A stack is a LIFO (Last In, First Out) data structure.
Elements are added and removed from the same end, called the top.
Stack Operations:
- push(item): Add an item to the top of the stack.
- pop(): Remove an item from the top of the stack.
- peek(): View the item at the top without removing it.
- isEmpty(): Check if the stack is empty.
What is a Queue?
A queue is a FIFO (First In, First Out) data structure.
Elements are added at the rear and removed from the front.
Queue Operations:
- enqueue(item): Add an item to the rear of the queue.
- dequeue(): Remove an item from the front of the queue.
- peek(): View the item at the front without removing it.
- isEmpty(): Check if the queue is empty.
How Can We Use Stacks and Queues for a Calculator?
Using a Stack in a Calculator:
Stacks are ideal for evaluating mathematical expressions, particularly those in postfix notation (Reverse Polish Notation), where operators follow operands.
Steps to Evaluate Postfix Expression using Stack:
- Read the expression from left to right.
- If an operand (number) is encountered, push it onto the stack.
- If an operator is encountered, pop two operands from the stack, apply the operator, and push the result back onto the stack.
- Continue this process until the end of the expression.
- The final result will be the only value left in the stack.
Example: 5 3 + 4 *
- Push
5→ Stack:[5] - Push
3→ Stack:[5, 3] - Encounter
+: Pop3and5, calculate5 + 3 = 8, push8→ Stack:[8] - Push
4→ Stack:[8, 4] - Encounter
*: Pop4and8, calculate8 * 4 = 32, push32→ Stack:[32] - Final result:
32
Using a Queue in a Calculator:
Queues are less commonly used for direct arithmetic calculations but can be useful in simulating processes like order of operations or handling multiple tasks.
For instance, a queue could be used in a multi-step calculator where tasks (like addition, subtraction, etc.) are added to the queue, and the system processes them in the order they were received.
Example: Using a Stack for Infix to Postfix Conversion
The following steps can be used to convert an infix expression (like 3 + 5 * 2) to postfix notation using a stack:
- Initialize an empty stack.
- Process the infix expression from left to right.
- If a number is encountered, add it to the output expression.
- If an operator is encountered, pop operators from the stack and add them to the output expression until an operator with lower precedence is found.
- Push the current operator onto the stack.
- At the end of the expression, pop any remaining operators in the stack and add them to the output.
For example:
- Infix:
3 + 5 * 2 - Postfix:
3 5 2 * +
Java code for infix to postfix notation
import java.util.Stack;
public class Calculator {
public static int prec(char c){
switch(c){
case '^':
return 3;
case '*':
return 2;
case '/':
return 2;
case '+':
return 1;
case '-':
return 1;
default:
return -1;
}
}
public static String infixToPostfix(String infix){
Stack<Character> charStack = new Stack<Character>();
String output = "";
for(int i = 0; i<infix.length();i++){
char j = infix.charAt(i);
if((int)j >=48 && (int)j <=57){ //numbers (operand)
output += j; //add operand to output
continue;
}
if((int)j >=65 && (int)j <=90){ //uppercase letters (operand)
output += j; //add operand to output
continue;
}
if((int)j >=97 && (int)j <=122){ //lowercase letters (operand)
output += j; //add operand to output
continue;
}
//start of a subsection
if(j=='('){
charStack.push(Character.valueOf(j));
continue;
}
//end of a subsection
if(j==')'){
while (!charStack.peek().equals(Character.valueOf('('))) {
output+=charStack.pop(); //add subsection to output
}
charStack.pop();
continue;
}
// while stack is not empty, and the preceding operator in the stack is a lower precedence in PEMDAS
while(!charStack.isEmpty() && (prec(j)<prec(charStack.peek().charValue())||prec(j)==prec(charStack.peek().charValue()))){
output += charStack.pop(); //remove current operator on the top of stack and add it to the output
}
charStack.push(Character.valueOf(j)); //add new operator to the stack
}
//empty stack in output
while(!charStack.isEmpty()){
output += charStack.pop();
}
//this gives us our postfix output
return output;
}
public static void main(String[] args) {
String expression = "1+2*(3^4-5)^(6+7*8)-9";
String post = infixToPostfix(expression);
System.out.println(expression);
System.out.println(post);
}
}
Calculator.main(null)
1+2*(3^4-5)^(6+7*8)-9
1234^5-678*+^*+9-
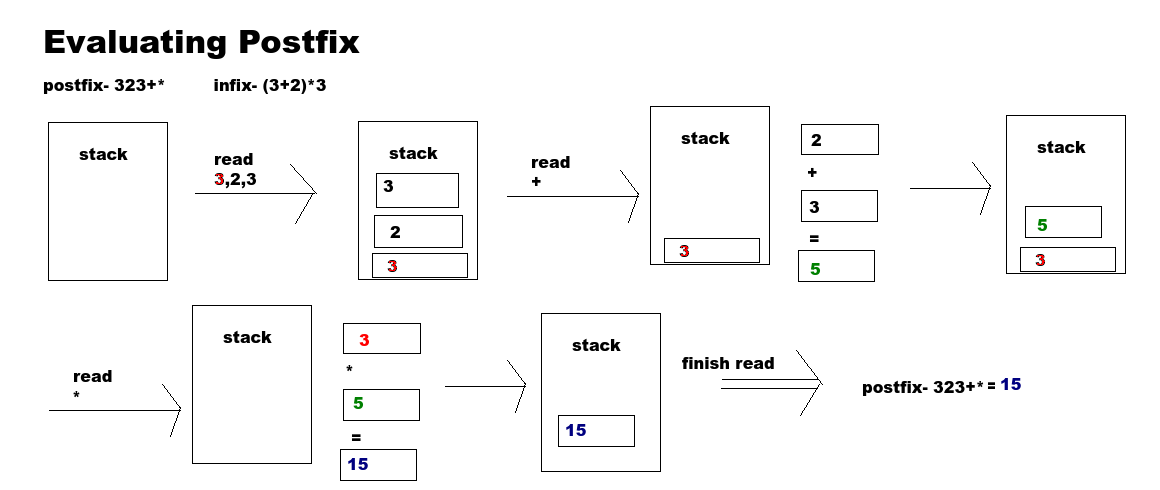
Evaulating Postfix with a Stack
We start with an expression that we convert to postfix
We move along the postfix string and for each step we do the following
if it is an operand (number), then we add it to the stack if it is an operator (+-*), then we pop the top 2 values of the stack and evalute using the expression. After evaulating the operation we add the solution onto the stack. When finished evaulting all operators and operands there will be 1 value left on the stack, that is our answer.
String postfix = "12+";
Stack<Double> stack = new Stack<Double>();
//Go through our queue (postfix string)
//step 1 check the first charater of the postfix
// we see that it is a number (operand) so we add it to the stack
if(postfix.substring(0,1).matches("\\d")){ //true
System.out.println("adding "+postfix.substring(0,1)+" to the stack");
stack.push(Double.valueOf(postfix.substring(0,1)));
}
//step 2 check the second charater of postfix
// we see that it is a number (operand) so we add it to the stack
if(postfix.substring(1,2).matches("\\d")){ //true
System.out.println("adding "+postfix.substring(1,2)+" to the stack");
stack.push(Double.valueOf(postfix.substring(1,2)));
}
//step 3 check the third character of the postfix
if(postfix.substring(2,3).matches("\\d")){ //false
}
else {
System.out.println("evaluating operator: "+postfix.substring(2,3));
double val1 = stack.pop().doubleValue(); //top of the stack
double val2 = stack.pop().doubleValue(); //next to the top of the stack
//evalute val1,val2 with the given operator
switch(postfix.substring(2,3)){
case "+":
System.out.println("adding evaluated: "+String.valueOf(val2+val1)+" to the stack");
stack.push(Double.valueOf(val2+val1)); //add the evalution to the stack
break;
//other operators here
}
};
//we have now gone through the entire postfix string
// since the stack has only 1 value left, we can assume it is the answer
System.out.println();
System.out.println(stack.peek().toString() + " is at the top of the stack"); //peek at the top of the stack
adding 1 to the stack
adding 2 to the stack
evaluating operator: +
adding evaluated: 3.0 to the stack
3.0 is at the top of the stack
how the actual function looks
double calculatePostfixExpression(String postfix){
Stack<Double> doubleStack = new Stack<Double>();
for(int i = 0; i<postfix.length();i++){
char j = postfix.charAt(i); //probally don't need to use charAt, just use substring
if((int)j >=48 && (int)j <=57){ //numbers (operand)
doubleStack.push(Double.valueOf(String.valueOf(j))); //cast char to String and then to a Double
}
else { //assume it is an operator
if(doubleStack.size()<2){ //avoid out of bounds errors
continue;
}
//pop top two values in the stack
double a = doubleStack.pop().doubleValue(); //top
double b = doubleStack.pop().doubleValue(); //second from top
//evaluate and place back on top of the stack
switch(j){
case '^':
doubleStack.push(Double.valueOf(Math.pow(b, a)));
break;
case '*':
doubleStack.push(Double.valueOf(b*a));
break;
case '/':
doubleStack.push(Double.valueOf(b/a));
break;
case '+':
doubleStack.push(Double.valueOf(b+a));
break;
case '-':
doubleStack.push(Double.valueOf(b-a));
break;
default: //unexepected value, so ill just put the stack back in place
doubleStack.push(Double.valueOf(b));
doubleStack.push(Double.valueOf(a));
}
}
}
return doubleStack.peek().doubleValue();
}
//solving for 1/(4*3+2) = 1/14 = ~.0714
double solution = calculatePostfixExpression("1234*+/");
System.out.println(solution);
0.07142857142857142
Example: Using a Queue for Order of Operations Simulation
A queue can simulate the process of handling different operations in a calculator where operations are processed in the order they were added. For instance:
- Enqueue tasks like
3 + 5,2 - 1, etc. - Dequeue and process each task in order.
- The queue ensures that the operations are executed in the correct sequence.
Java Code for Queue Simulation
import java.util.LinkedList;
import java.util.Queue;
public class CalculatorQueue {
public static void main(String[] args) {
// Create a queue to store operations
Queue<String> operations = new LinkedList<>();
// Enqueue tasks
operations.add("3 + 5");
operations.add("2 - 1");
// Process tasks in order
while (!operations.isEmpty()) {
String operation = operations.poll(); // Dequeue
System.out.println("Processing: " + operation);
// In a real calculator, here you'd process the operation
}
}
}
CalculatorQueue.main(null)
Processing: 3 + 5
Processing: 2 - 1
Homework (hw)
- Queue Task: Modify the CalculatorQueue to support more complex operations, such as multiplication and division.
- Stack Task: Modify the CalculatorStack to reverse the order of addition and handle operations in the LIFO sequence.
- Add a method to both the stack and queue programs to handle invalid operations and display an error message.
- Create a method for both programs to display all operations before processing them, and track the result after each operation.
- Advanced Task: Implement a calculator that supports parentheses using a stack to ensure proper operation precedence.
Postfix evaulation using an array (this allows numbers to be more than 0-9)
double calculatePostfixExpressionArray(String[] postfix){
Stack<Double> doubleStack = new Stack<Double>();
for(int i = 0; i<postfix.length;i++){
String j = postfix[i];
if (j.matches("-?\\d+")) {
doubleStack.push(Double.valueOf(j)); //cast String to a Double
}
else { //assume it is an operator
if(doubleStack.size()<2){ //avoid out of bounds errors
continue;
}
//pop top two values in the stack
double a = doubleStack.pop().doubleValue(); //top
double b = doubleStack.pop().doubleValue(); //second from top
//evaluate and place back on top of the stack
switch(j){
case "^":
doubleStack.push(Double.valueOf(Math.pow(b, a)));
break;
case "*":
doubleStack.push(Double.valueOf(b*a));
break;
case "/":
doubleStack.push(Double.valueOf(b/a));
break;
case "+":
doubleStack.push(Double.valueOf(b+a));
break;
case "-":
doubleStack.push(Double.valueOf(b-a));
break;
default: //unexepected value, so ill just put the stack back in place
doubleStack.push(Double.valueOf(b));
doubleStack.push(Double.valueOf(a));
}
}
}
return doubleStack.peek().doubleValue();
}
//solving for 10/2 = 5
String[] arr = {"10","2","/"};
double solution = calculatePostfixExpressionArray(arr);
System.out.println(solution)
5.0
