Sorting/Searching Algorithms - Sorting Lesson

Sorting Algorithms

Big O Notation:

• Measures how fast algorithms run as input size grows
• Shows worst-case performance scenario
• Ignores constants and focuses on growth rate
• Common notations:
  • O(1): Constant time (same speed regardless of input size)
  • O(log n): Logarithmic (gets slightly slower with larger inputs)
  • O(n): Linear time (speed directly proportional to input size)
  • O(n log n): Common in efficient sorting algorithms
  • O(n²): Quadratic time (common in nested loops)
  • O(2ⁿ): Exponential time (very slow for large inputs)
• Helps compare efficiency of different algorithms
• Used to make decisions about which algorithm to implement

1. Selection Sorting

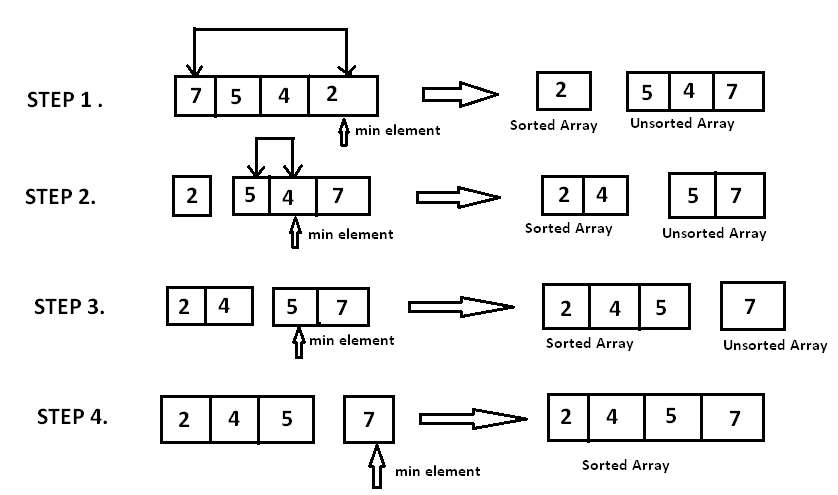
Selection sort methodically builds the sorted list by repeatedly finding and placing the smallest remaining element.

• Finds the smallest element in the unsorted portion
• Swaps it with the first unsorted element
• Repeats until the entire list is sorted
• Makes fewer swaps than bubble sort

public class SelectionSort {
    public static void main(String[] args) {
        int[] list = {28, 12, 18, 8, 30, 3, 17, 14};
        
        System.out.println("Sorting process:");
        for (int currentIndex = 0; currentIndex < list.length - 1; currentIndex++) {
            int minIndex = currentIndex;
            
            // Find the minimum element in the unsorted part
            for (int i = currentIndex + 1; i < list.length; i++) {
                if (list[i] < list[minIndex]) {
                    minIndex = i;
                }
            }
            
            // Swap the current element with the minimum element
            int temp = list[currentIndex];
            list[currentIndex] = list[minIndex];
            list[minIndex] = temp;

            // Print the array after each swap
            printArray(list);
        }
        
        System.out.println("\nFinal sorted list:");
        printArray(list);
    }

    // Helper method to print the array
    private static void printArray(int[] array) {
        for (int num : array) {
            System.out.print(num + " ");
        }
        System.out.println();
    }
}

SelectionSort.main(new String[]{});

Sorting process:
3 12 18 8 30 28 17 14 
3 8 18 12 30 28 17 14 
3 8 12 18 30 28 17 14 
3 8 12 14 30 28 17 18 
3 8 12 14 17 28 30 18 
3 8 12 14 17 18 30 28 
3 8 12 14 17 18 28 30 

Final sorted list:
3 8 12 14 17 18 28 30 

2. Insertion Sorting

Insertion sort mimics how we naturally sort items like playing cards by building the sorted list one element at a time.

• Builds the sorted list one item at a time
• Takes each element and inserts it into its correct position among already sorted elements
• Works well for small data sets or nearly sorted data
• Similar to how people typically sort playing cards

Code Example:

public class InsertionSort {
    public static void main(String[] args) {
        int[] list = {28, 12, 18, 8, 30, 3, 17, 14};
        
        System.out.println("Sorting process:");
        
        // Insertion sort algorithm
        for (int i = 1; i < list.length; i++) {
            int currentValue = list[i];
            int j = i - 1;
            
            // Shift larger elements to the right
            while (j >= 0 && list[j] > currentValue) {
                list[j + 1] = list[j];
                j--;
            }
            
            // Place the current value in the correct position
            list[j + 1] = currentValue;
            
            // Print the list after each insertion
            for (int k = 0; k < list.length; k++) {
                System.out.print(list[k] + " ");
            }
            System.out.println();  // New line after each pass
        }

        // Final sorted list
        System.out.println("Sorted array:");
        for (int num : list) {
            System.out.print(num + " ");
        }
    }
}

InsertionSort.main(new String[]{});

Sorting process:
12 28 18 8 30 3 17 14 
12 18 28 8 30 3 17 14 
8 12 18 28 30 3 17 14 
8 12 18 28 30 3 17 14 
3 8 12 18 28 30 17 14 
3 8 12 17 18 28 30 14 
3 8 12 14 17 18 28 30 
Sorted array:
3 8 12 14 17 18 28 30